Math Puzzle: Play Architect with These Homes of Playing cards
Jovan constructed these 5 homes of playing cards utilizing a complete of precisely 90 taking part in playing cards. Now he needs to construct one massive home consisting of precisely 100 playing cards. Can such a home of playing cards exist?
Amanda Montañez; Supply: Hans-Karl Eder/Spektrum der Wissenschaft (reference)
You possibly can construct a home of playing cards with precisely 100 playing cards; it can have eight flooring.
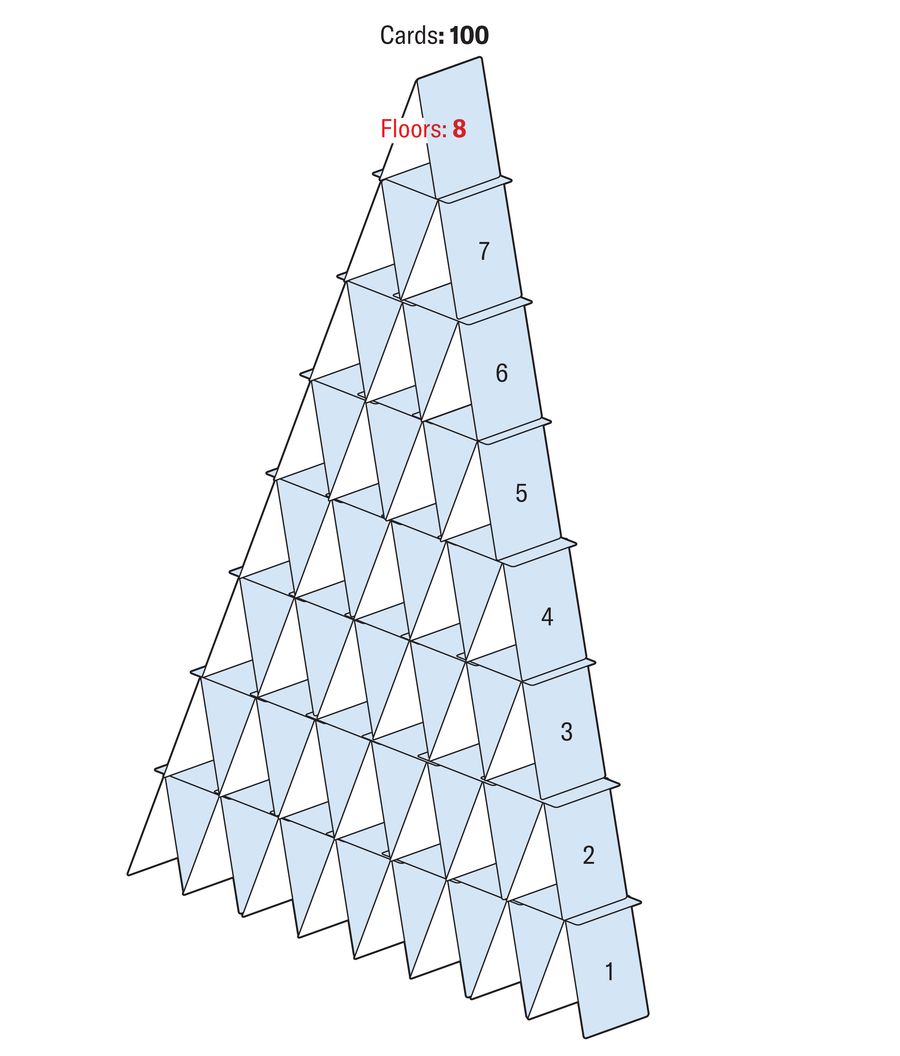
Amanda Montañez; Supply: Hans-Karl Eder/Spektrum der Wissenschaft (reference)
The variety of playing cards will increase stage by stage in a continuing sequence. If you wish to show the puzzle’s reply, it’s a must to present that 100 is a time period on this sequence.
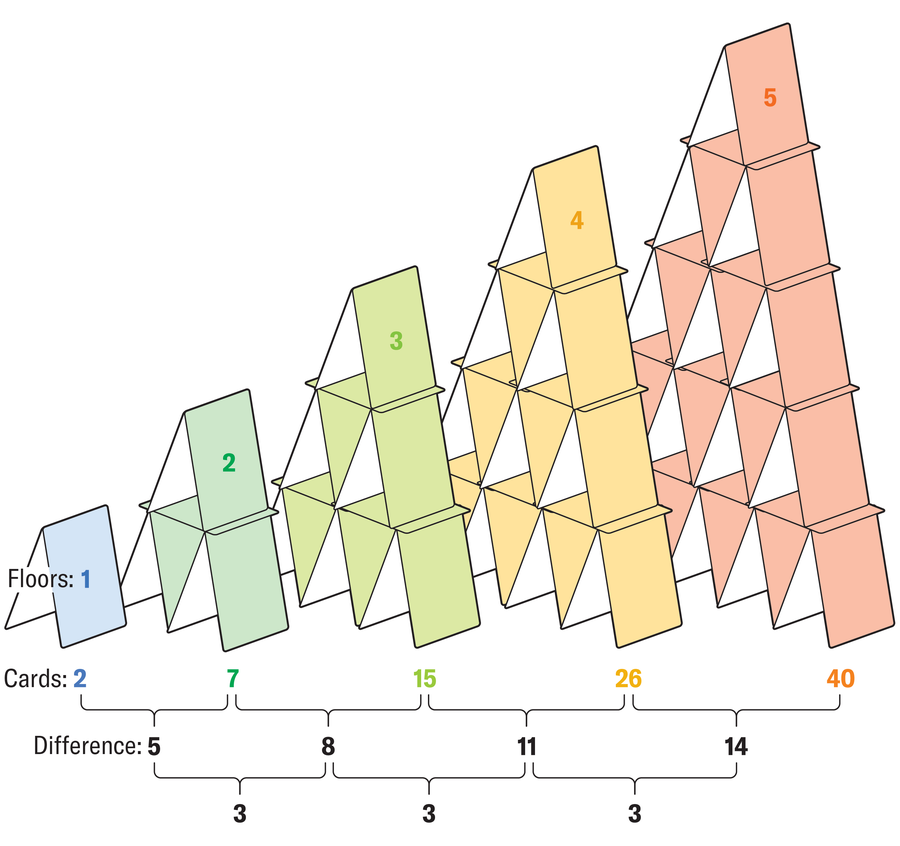
Amanda Montañez; Supply: Hans-Karl Eder/Spektrum der Wissenschaft (reference)
As a result of the distinction between phrases at all times modifications the identical quantity—the “second difference” is fixed—you’ll be able to conclude that the sequence, with variety of playing cards Okay and variety of rows x, will be represented by a quadratic equation of the shape Okay = ax2 + bx + c.
First, decide the values for a, b and c. This may be achieved utilizing a system of three equations:

Amanda Montañez; Supply: Hans-Karl Eder/Spektrum der Wissenschaft (reference)
With the values discovered for a, b and c and the calculated worth for Okay = 100, now you can clear up the quadratic equation.

Amanda Montañez; Supply: Hans-Karl Eder/Spektrum der Wissenschaft (reference)
One of many values for x is a pure quantity that permits you to construct a home of playing cards out of precisely 100 playing cards.
We’d love to listen to from you! E-mail us at video games@sciam.com to share your expertise.
This puzzle initially appeared in Spektrum der Wissenschaft and was reproduced with permission.

