Should you had to decide on just a few phrases or symbols to encapsulate your legacy, what would you decide? Johann Carl Friedrich Gauss (1777–1855) left behind a trophy case stocked with mathematical achievements to select from, however above all, he needed a “regular heptadecagon” etched on his gravestone. The extremely symmetrical 17-sided form starred in a proof that Gauss thought-about certainly one of his best contributions to math. At simply 18 years outdated Gauss used a heptadecagon to unravel a traditional drawback that had stumped mathematicians for greater than 2,000 years. A tour via that historical past reveals deep connections between the traditional conception of shapes as drawings and a contemporary perspective of the equations that govern them.
Historical Greek Geometry
The historic Greeks excelled at geometry, inserting particular emphasis on constructions created with a compass and straightedge. Consider these constructions as diagrams with desired geometric properties created solely with a writing utensil and two instruments. Given two factors, a compass (to not be confused with the navigational machine) attracts a circle centered at both level that passes via the opposite level. A straightedge attracts straight strains between the factors. Neither device has any markings on it, so they can not measure distances or angles.
On supporting science journalism
Should you’re having fun with this text, think about supporting our award-winning journalism by subscribing. By buying a subscription you’re serving to to make sure the way forward for impactful tales in regards to the discoveries and concepts shaping our world right this moment.
The Greeks didn’t impose arbitrary guidelines simply to make math tougher. The sport of setting up shapes with a compass and straightedge originates in Euclid’s Components, one of the essential textbooks ever written. Like fashionable mathematicians, Euclid got down to derive all of geometry from a minimal checklist of assumptions known as postulates. As a substitute of merely asserting the existence of shapes or different geometric objects, Euclid needed to construct them explicitly from the best components: strains and circles.
To get a really feel for these constructions, attempt one for your self. Given the road phase from A to B beneath, discover its midpoint. Eyeballing gained’t suffice; your methodology should discover the precise midpoint.
First use the compass to attract a circle centered at A and passing via B (first panel). Then repeat this step with the circle centered at B and passing via A (second panel). These circles intersect at two factors. Use the straightedge to attach these factors (third panel). By the symmetry in our building, this vertical line will intersect the unique line phase precisely at its midpoint.
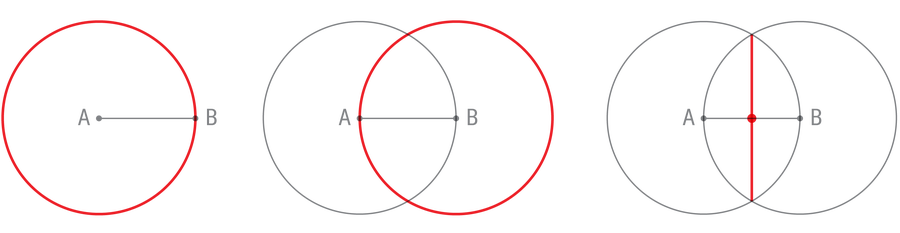
This building does rather more than bisect a line phase. It creates a proper angle between the 2 strains, which isn’t a trivial feat with such a restricted device set. And by connecting just a few extra factors, you can also make an equilateral triangle—one whose sides have equal lengths (and whose angles have equal measure).
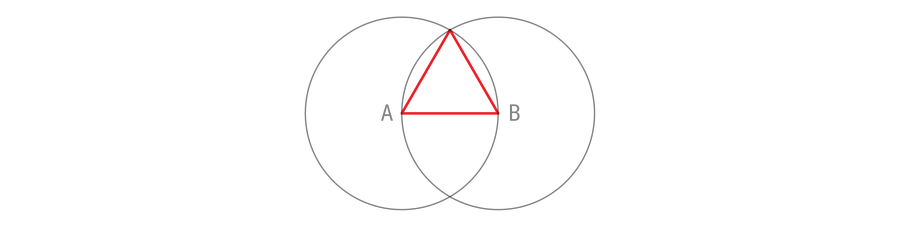
Discover that every fringe of the triangle can be a radius of one of many circles. The circles are the identical dimension and subsequently all of the triangle’s sides have the identical size. So equilateral triangles are constructible with a compass and straightedge, QED. Congratulations on persisting via the first proposition within the first e-book of Euclid’s Components. Solely 13 extra books to go.
A Roadblock
Of all of the shapes that one can assemble with a compass and straightedge, common polygons maintain a particular cachet. Polygons are enclosed shapes composed of straight-line edges, equivalent to triangles and rectangles (versus curved shapes equivalent to circles or unenclosed shapes such because the letter E). Common polygons have essentially the most symmetry in that their sides all have equal size and their angles all have equal measure (like squares and equilateral triangles however not like rectangles and rhombuses). Setting up any outdated irregular triangle with a compass and straightedge is youngster’s play—simply scatter three factors on the web page and join them with strains. However setting up our completely symmetric equilateral triangle—a daily polygon—required some elegant legwork.
Euclid found out assemble common polygons with three, 4 and 5 sides—or equilateral triangles, squares and common pentagons, respectively. He squeezed just a few extra generalizations out of those core constructions; as an example, after you have a daily polygon on the web page, a easy maneuver will produce a brand new common polygon with double the variety of sides.
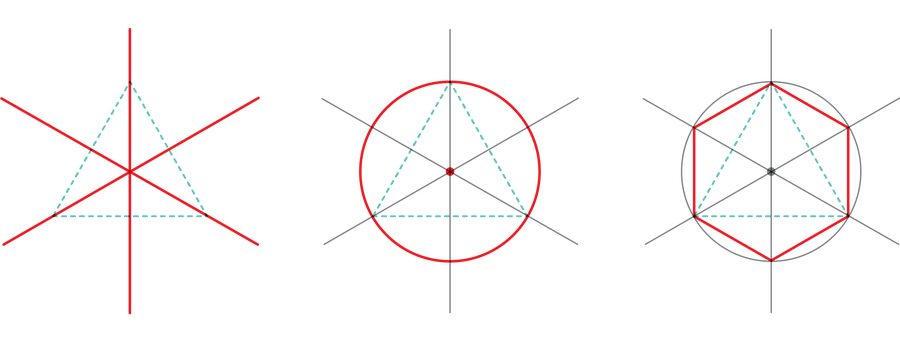
You’ll be able to repeat this doubling process as many instances as you would like. Meaning three-, four- and five-sided common polygons could be remodeled into six-, eight- and 10-sided common polygons, in addition to 12-, 16- and 20-sided ones, and so forth. Euclid additionally confirmed “multiply” the three- and five-sided common polygons to provide a common 15-gon.
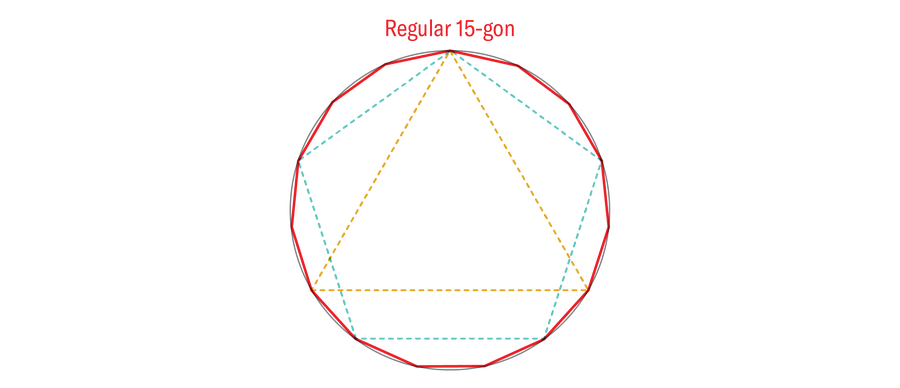
Progress halted there. Someway Euclid knew {that a} common 3,072-gon was constructible in precept (a triangle doubled 10 instances), however he had no concept assemble a daily seven-gon (heptagon) or 11-gon (hendecagon). To be clear, common polygons of any variety of sides better than two do exist and could be constructed with extra succesful instruments. The query that Euclid left behind asks which of them are constructible with a compass and straightedge alone. This query would stay unanswered for 2 millennia till a sure German teenager picked up a pencil.
18th-Century Math to the Rescue
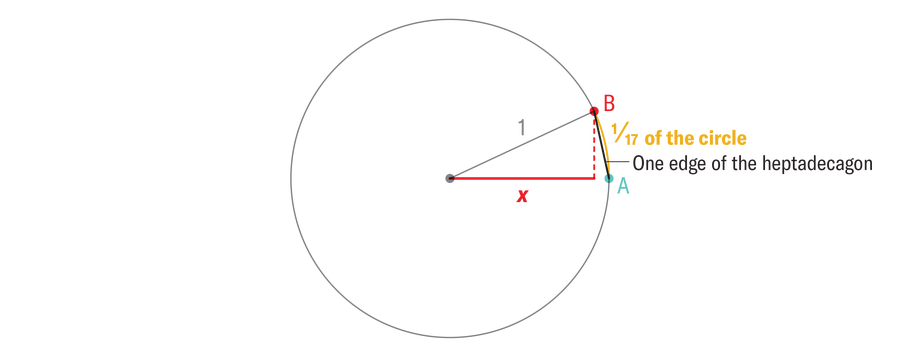
By 1796 no new common polygons had joined the pantheon of constructible shapes, but mathematicians had acquired a deeper understanding of compass and straightedge constructions. Gauss knew scale back the issue of setting up a daily polygon to that of merely setting up a line phase with a really particular size. To see create a 17-gon, begin with a unit circle (the place the radius equals one) and some extent A on the circle. Think about we might discover the purple level B above A precisely one seventeenth of the way in which across the circle. If we might assemble the purple level from the blue level, we might repeat that building all the way in which across the circle, join the dots with our straightedge, and voilà, a daily heptadecagon. How can we draw level B, given level A, although? Discover that if we might draw the purple line phase labeled x, then we are able to hint that as much as the purple level B, and we win. Your entire drawback of setting up a daily heptadecagon boils right down to setting up a line phase with the exact size x. For the mathematically curious, x = cosine (2π ⁄17).
Can a compass and straightedge assemble a line phase of any size? By Gauss’s time, mathematicians knew the stunning reply to this query. A size is constructible precisely when it may be expressed with the operations of addition, subtraction, multiplication, division or sq. roots utilized to integers. So some unusual numbers such because the sq. root of 99⁄5 are constructible (99 and 5 are integers, and we’ve utilized division and sq. root to them), whereas some extra acquainted numbers equivalent to pi (π) and the dice root of two can’t be constructed as a result of one can by no means write them by way of these 5 operations alone.
Remarkably, the rudimentary instruments that the traditional Greeks used to attract their geometric diagrams completely match the pure operations of modern-day algebra: addition (+), subtraction (–), multiplication (x), division (/) and taking sq. roots (√). The rationale stems from the truth that the equations for strains and circles solely use these 5 operations, a perspective that Euclid couldn’t have envisioned within the prealgebra age.
It’d shock you to be taught that Gauss by no means truly drew a daily heptadecagon. He didn’t have to. He proved that the form is constructible in precept by expressing the particular size x [cosine (2π ⁄17)] solely by way of the 5 algebraic operations that the compass and straightedge allow. Even should you don’t discover his equation notably enlightening, its complexity demonstrates how a lot work the adolescent should have poured into the issue:

Much more spectacular, Gauss totally characterised which common polygons are constructible and which aren’t (though it was not till 1837 that Pierre Wantzel offered a rigorous proof that Gauss’s characterization didn’t miss something). So not solely did Gauss describe the shape that each one constructible common polygons take, he and Wantzel vindicated Euclid’s frustrations by proving that the elusive common heptagon (seven sides) and hendecagon (11 sides) are unimaginable to assemble with a compass and straightedge alone, together with infinitely many different shapes.
Based on biographer G. Waldo Dunnington, Gauss felt nice satisfaction in cracking the millennia-old drawback and advised a good friend that he needed a daily heptadecagon displayed on his gravestone. Sadly, this didn’t occur, however a monument in Gauss’s start metropolis of Brunswick, Germany, boasts a 17-pointed star engraved on the again. The stonemason selected a star as a result of he believed that folks couldn’t distinguish a heptadecagon from a circle. I ponder if Euclid would agree.

