Picture by Writer
Outliers are irregular observations that differ considerably from the remainder of your information. They might happen on account of experimentation error, measurement error, or just that variability is current inside the information itself. These outliers can severely impression your mannequin’s efficiency, resulting in biased outcomes – very similar to how a prime performer in relative grading at universities can increase the common and have an effect on the grading standards. Dealing with outliers is an important a part of the information cleansing process.
On this article, I will share how one can spot outliers and other ways to cope with them in your dataset.
Detecting Outliers
There are a number of strategies used to detect outliers. If I had been to categorise them, right here is the way it appears to be like:
- Visualization-Based mostly Strategies: Plotting scatter plots or field plots to see information distribution and examine it for irregular information factors.
- Statistics-Based mostly Strategies: These approaches contain z scores and IQR (Interquartile Vary) which provide reliability however could also be much less intuitive.
I will not cowl these strategies extensively to remain targeted, on the subject. Nonetheless, I will embody some references on the finish, for exploration. We are going to use the IQR technique in our instance. Right here is how this technique works:
IQR (Interquartile Vary) = Q3 (seventy fifth percentile) – Q1 (twenty fifth percentile)
The IQR technique states that any information factors beneath Q1 – 1.5 * IQR or above Q3 + 1.5 * IQR are marked as outliers. Let’s generate some random information factors and detect the outliers utilizing this technique.
Make the required imports and generate the random information utilizing np.random:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Generate random information
np.random.seed(42)
information = pd.DataFrame({
'worth': np.random.regular(0, 1, 1000)
})
Detect the outliers from the dataset utilizing the IQR Methodology:
# Operate to detect outliers utilizing IQR
def detect_outliers_iqr(information):
Q1 = information.quantile(0.25)
Q3 = information.quantile(0.75)
IQR = Q3 - Q1
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
return (information upper_bound)
# Detect outliers
outliers = detect_outliers_iqr(information['value'])
print(f"Number of outliers detected: {sum(outliers)}")
Output ⇒ Variety of outliers detected: 8
Visualize the dataset utilizing scatter and field plots to see the way it appears to be like
# Visualize the information with outliers utilizing scatter plot and field plot
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# Scatter plot
ax1.scatter(vary(len(information)), information['value'], c=['blue' if not x else 'red' for x in outliers])
ax1.set_title('Dataset with Outliers Highlighted (Scatter Plot)')
ax1.set_xlabel('Index')
ax1.set_ylabel('Worth')
# Field plot
sns.boxplot(x=information['value'], ax=ax2)
ax2.set_title('Dataset with Outliers (Field Plot)')
ax2.set_xlabel('Worth')
plt.tight_layout()
plt.present()
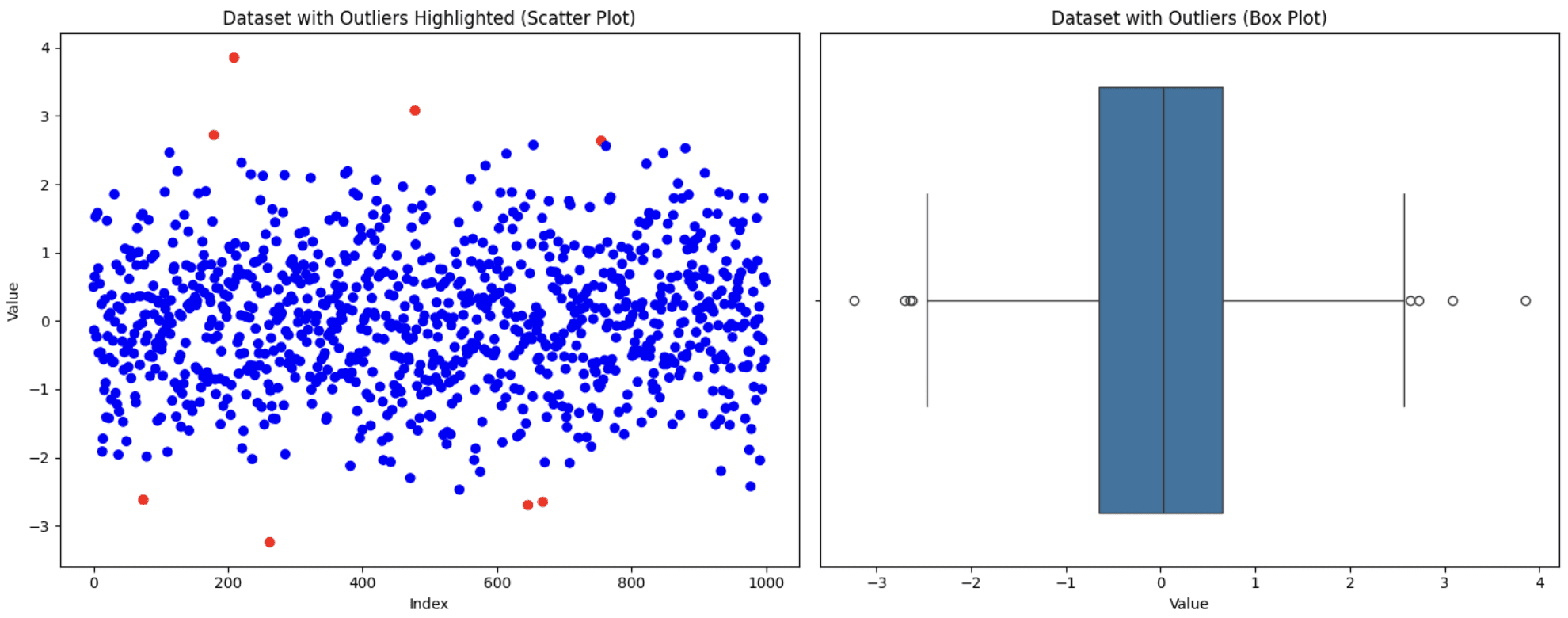
Unique Dataset
Now that we have now detected the outliers, let’s talk about among the other ways to deal with the outliers.
Dealing with Outliers
1. Eradicating Outliers
This is among the easiest approaches however not all the time the appropriate one. You have to contemplate sure components. If eradicating these outliers considerably reduces your dataset measurement or in the event that they maintain helpful insights, then excluding them out of your evaluation not be essentially the most favorable choice. Nonetheless, in the event that they’re on account of measurement errors and few in quantity, then this strategy is appropriate. Let’s apply this system to the dataset generated above:
# Take away outliers
data_cleaned = information[~outliers]
print(f"Original dataset size: {len(data)}")
print(f"Cleaned dataset size: {len(data_cleaned)}")
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# Scatter plot
ax1.scatter(vary(len(data_cleaned)), data_cleaned['value'])
ax1.set_title('Dataset After Eradicating Outliers (Scatter Plot)')
ax1.set_xlabel('Index')
ax1.set_ylabel('Worth')
# Field plot
sns.boxplot(x=data_cleaned['value'], ax=ax2)
ax2.set_title('Dataset After Eradicating Outliers (Field Plot)')
ax2.set_xlabel('Worth')
plt.tight_layout()
plt.present()
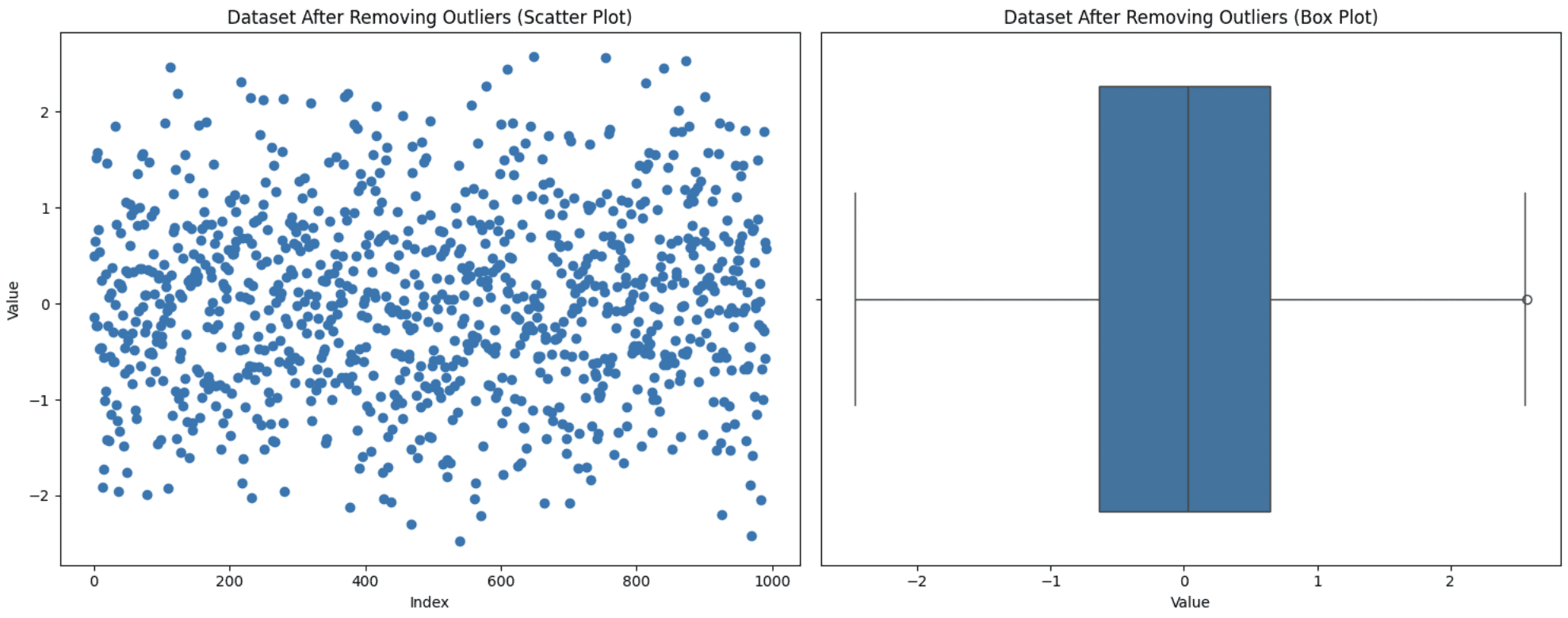
Eradicating Outliers
Discover that the distribution of the information can really be modified by eradicating outliers. When you take away some preliminary outliers, the definition of what’s an outlier might very properly change. Due to this fact, information that might have been within the regular vary earlier than, could also be thought of outliers below a brand new distribution. You possibly can see a brand new outlier with the brand new field plot.
2. Capping Outliers
This method is used when you do not need to discard your information factors however maintaining these excessive values may impression your evaluation. So, you set a threshold for the utmost and the minimal values after which carry the outliers inside this vary. You possibly can apply this capping to outliers or to your dataset as a complete too. Let’s apply the capping technique to our full dataset to carry it inside the vary of the Fifth-Ninety fifth percentile. Right here is how one can execute this:
def cap_outliers(information, lower_percentile=5, upper_percentile=95):
lower_limit = np.percentile(information, lower_percentile)
upper_limit = np.percentile(information, upper_percentile)
return np.clip(information, lower_limit, upper_limit)
information['value_capped'] = cap_outliers(information['value'])
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# Scatter plot
ax1.scatter(vary(len(information)), information['value_capped'])
ax1.set_title('Dataset After Capping Outliers (Scatter Plot)')
ax1.set_xlabel('Index')
ax1.set_ylabel('Worth')
# Field plot
sns.boxplot(x=information['value_capped'], ax=ax2)
ax2.set_title('Dataset After Capping Outliers (Field Plot)')
ax2.set_xlabel('Worth')
plt.tight_layout()
plt.present()
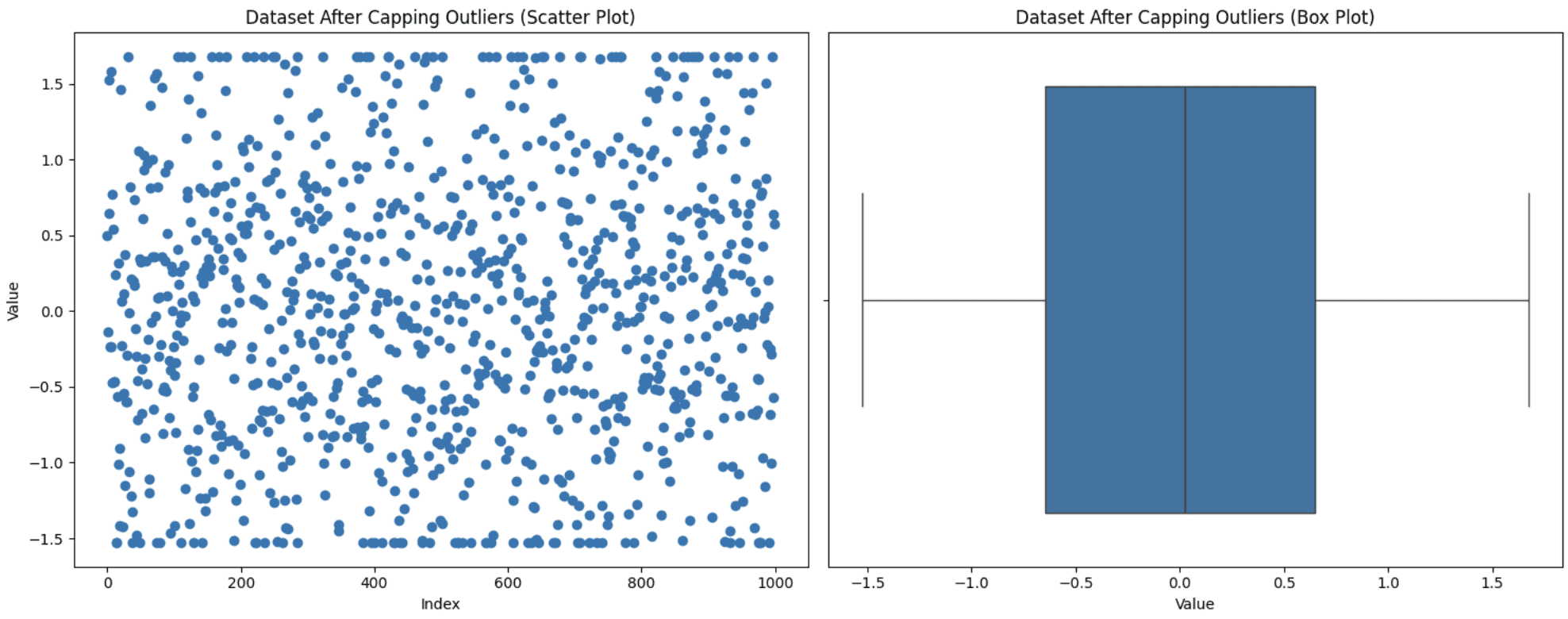
Capping Outliers
You possibly can see from the graph that the higher and decrease factors within the scatter plot seem like in a line on account of capping.
3. Imputing Outliers
Generally eradicating values from the evaluation is not an choice as it could result in data loss, and also you additionally don’t need these values to be set to max or min like in capping. On this state of affairs, one other strategy is to substitute these values with extra significant choices like imply, median, or mode. The selection varies relying on the area of information below remark, however be conscious of not introducing biases whereas utilizing this system. Let’s exchange our outliers with the mode (essentially the most ceaselessly occurring worth) worth and see how the graph seems:
information['value_imputed'] = information['value'].copy()
median_value = information['value'].median()
information.loc[outliers, 'value_imputed'] = median_value
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# Scatter plot
ax1.scatter(vary(len(information)), information['value_imputed'])
ax1.set_title('Dataset After Imputing Outliers (Scatter Plot)')
ax1.set_xlabel('Index')
ax1.set_ylabel('Worth')
# Field plot
sns.boxplot(x=information['value_imputed'], ax=ax2)
ax2.set_title('Dataset After Imputing Outliers (Field Plot)')
ax2.set_xlabel('Worth')
plt.tight_layout()
plt.present()
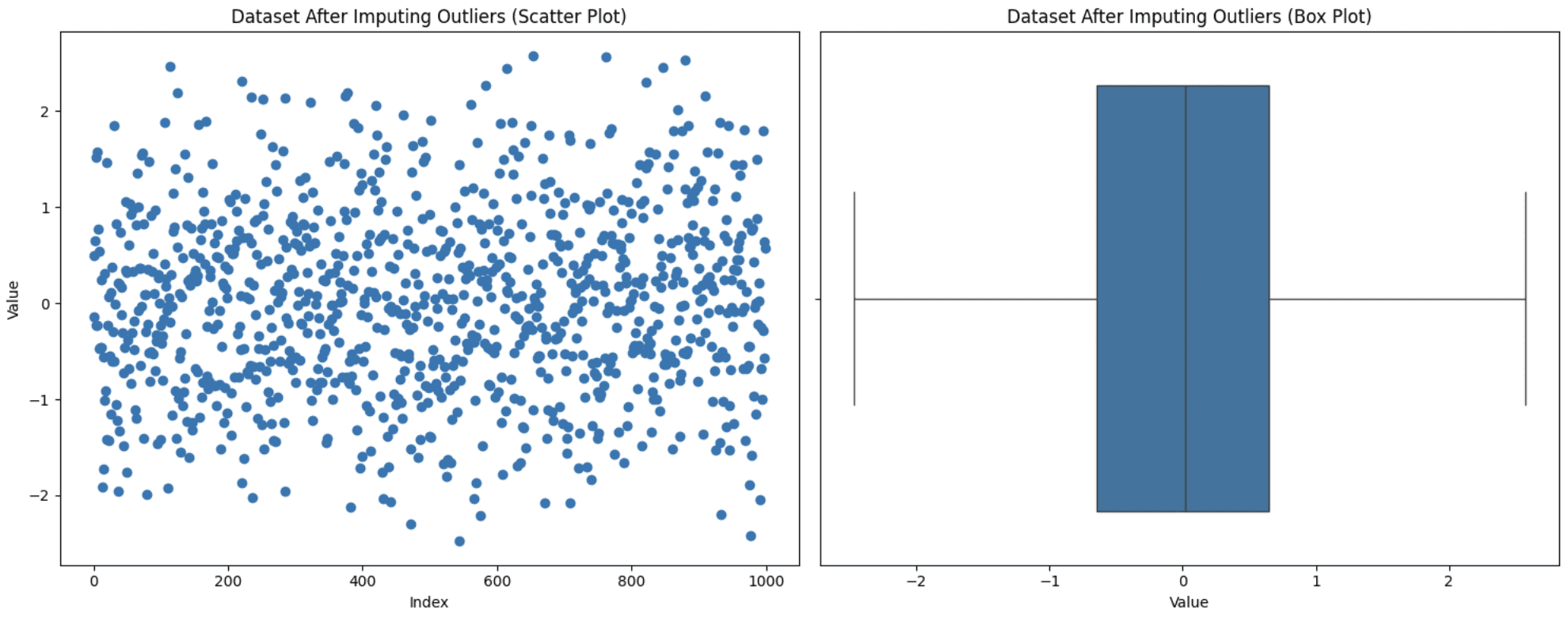
Imputing Outliers
Discover that now we have no outliers, however this does not assure that outliers will probably be eliminated since after the imputation, the IQR additionally modifications. You have to experiment to see what matches greatest on your case.
4. Making use of a Transformation
Transformation is utilized to your full dataset as an alternative of particular outliers. You mainly change the best way your information is represented to scale back the impression of the outliers. There are a number of transformation strategies like log transformation, sq. root transformation, box-cox transformation, Z-scaling, Yeo-Johnson transformation, min-max scaling, and many others. Selecting the best transformation on your case will depend on the character of the information and your finish aim of the evaluation. Listed here are a number of ideas that can assist you choose the appropriate transformation approach:
- For right-skewed information: Use log, sq. root, or Field-Cox transformation. Log is even higher once you wish to compress small quantity values which are unfold over a big scale. Sq. root is best when, other than proper skew, you desire a much less excessive transformation and likewise wish to deal with zero values, whereas Field-Cox additionally normalizes your information, which the opposite two do not.
- For left-skewed information: Replicate the information first after which apply the strategies talked about for right-skewed information.
- To stabilize variance: Use Field-Cox or Yeo-Johnson (just like Field-Cox however handles zero and unfavorable values as properly).
- For mean-centering and scaling: Use z-score standardization (commonplace deviation = 1).
- For range-bound scaling (fastened vary i.e., [2,5]): Use min-max scaling.
Let’s generate a right-skewed dataset and apply the log transformation to the whole information to see how this works:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Generate right-skewed information
np.random.seed(42)
information = np.random.exponential(scale=2, measurement=1000)
df = pd.DataFrame(information, columns=['value'])
# Apply Log Transformation (shifted to keep away from log(0))
df['log_value'] = np.log1p(df['value'])
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
# Unique Knowledge - Scatter Plot
axes[0, 0].scatter(vary(len(df)), df['value'], alpha=0.5)
axes[0, 0].set_title('Unique Knowledge (Scatter Plot)')
axes[0, 0].set_xlabel('Index')
axes[0, 0].set_ylabel('Worth')
# Unique Knowledge - Field Plot
sns.boxplot(x=df['value'], ax=axes[0, 1])
axes[0, 1].set_title('Unique Knowledge (Field Plot)')
axes[0, 1].set_xlabel('Worth')
# Log Reworked Knowledge - Scatter Plot
axes[1, 0].scatter(vary(len(df)), df['log_value'], alpha=0.5)
axes[1, 0].set_title('Log Reworked Knowledge (Scatter Plot)')
axes[1, 0].set_xlabel('Index')
axes[1, 0].set_ylabel('Log(Worth)')
# Log Reworked Knowledge - Field Plot
sns.boxplot(x=df['log_value'], ax=axes[1, 1])
axes[1, 1].set_title('Log Reworked Knowledge (Field Plot)')
axes[1, 1].set_xlabel('Log(Worth)')
plt.tight_layout()
plt.present()

Making use of Log Transformation
You possibly can see {that a} easy transformation has dealt with many of the outliers itself and decreased them to only one. This reveals the ability of transformation in dealing with outliers. On this case, it’s essential to be cautious and know your information properly sufficient to decide on acceptable transformation as a result of failing to take action might trigger issues for you.
Wrapping Up
This brings us to the tip of our dialogue about outliers, other ways to detect them, and find out how to deal with them. This text is a part of the pandas collection, and you may examine different articles on my creator web page. As talked about above, listed below are some further assets so that you can research extra about outliers:
- Outlier detection strategies in Machine Studying
- Completely different transformations in Machine Studying
- Varieties Of Transformations For Higher Regular Distribution
Kanwal Mehreen Kanwal is a machine studying engineer and a technical author with a profound ardour for information science and the intersection of AI with medication. She co-authored the book “Maximizing Productivity with ChatGPT”. As a Google Era Scholar 2022 for APAC, she champions range and tutorial excellence. She’s additionally acknowledged as a Teradata Range in Tech Scholar, Mitacs Globalink Analysis Scholar, and Harvard WeCode Scholar. Kanwal is an ardent advocate for change, having based FEMCodes to empower girls in STEM fields.

