How a Secret Society Found Irrational Numbers
Myths and legends encompass the origins of those numbers
The Pythagoreans had been thought of a type of cult – the members had been persecuted and killed.
Jakub Krechowicz/Alamy Inventory Photograph
The traditional scholar Hippasus of Metapontum was punished with loss of life for his discovery of irrational numbers—or not less than that’s the legend. What really occurred within the fifth century B.C.E. is much from clear.
Hippasus was a Pythagorean, a member of a sect that handled arithmetic and quantity mysticism, amongst different issues. A core ingredient of the Pythagoreans’ teachings associated to harmonic numerical relationships, which included fractions of complete numbers.
The entire world, they believed, may very well be described utilizing rational numbers, together with pure numbers and fractions. But when Hippasus examined the size ratios of a pentagram—the image of the Pythagoreans—the story goes, he realized that a few of the lengths of the form’s sides couldn’t be expressed as fractions. He thus offered the primary proof of the existence of irrational numbers.
On supporting science journalism
For those who’re having fun with this text, take into account supporting our award-winning journalism by subscribing. By buying a subscription you might be serving to to make sure the way forward for impactful tales in regards to the discoveries and concepts shaping our world at present.
From right here, the accounts of Hippasus diverge. Some say that the Pythagoreans took offense at this assertion as a result of such numbers went in opposition to their worldview. In different tales, Hippasus made his outcomes public and thus violated the sect’s secrecy. Both means, he drowned within the sea after his discovery. Some experiences declare that the Pythagoreans threw him off a ship. Others assert that his loss of life was an accident that the Pythagoreans considered divine punishment.
Present interpretations of the obtainable historic proof, nonetheless, recommend that these tales are pure legend. Hippasus’ discovery—assuming he even made it—was prone to have been hailed as a mathematical achievement that made the Pythagoreans proud. In actual fact, many questionable tales swirl across the Pythagoreans who had been persecuted for his or her philosophical and political concepts.
The obtainable information are restricted. The neighborhood was most likely based in what’s now southern Italy by Pythagoras of Samos—the Greek scholar after whom the well-known Pythagorean theorem is known as (though it’s also unclear whether or not he proved the concept). Along with their curiosity in arithmetic, the Pythagoreans had various views that set them aside from others in historical Greece. They rejected wealth, lived a vegetarian, ascetic way of life and believed in reincarnation. Ultimately, the group suffered a number of assaults and, after Pythagoras’ loss of life, the neighborhood disappeared fully.
Concerning the story of Hippasus, the ingredient that historians agree is most probably true is that the Pythagoreans in some unspecified time in the future proved the incommensurability of sure portions, from which the existence of irrational numbers follows.
Numbers past Fractions
We now study in class that some values—the so-called irrational numbers—can’t be expressed because the ratio of two integers. However this realization is much from apparent. In any case, irrational values can not less than be approximated by fractions—though that’s generally tough.
The famed proof of irrational numbers introduced by Hippasus—or one other Pythagorean—is most simply illustrated with an isosceles proper triangle: take into account a triangle with two sides, every of size a, that kind a proper angle reverse a hypotenuse of size c.
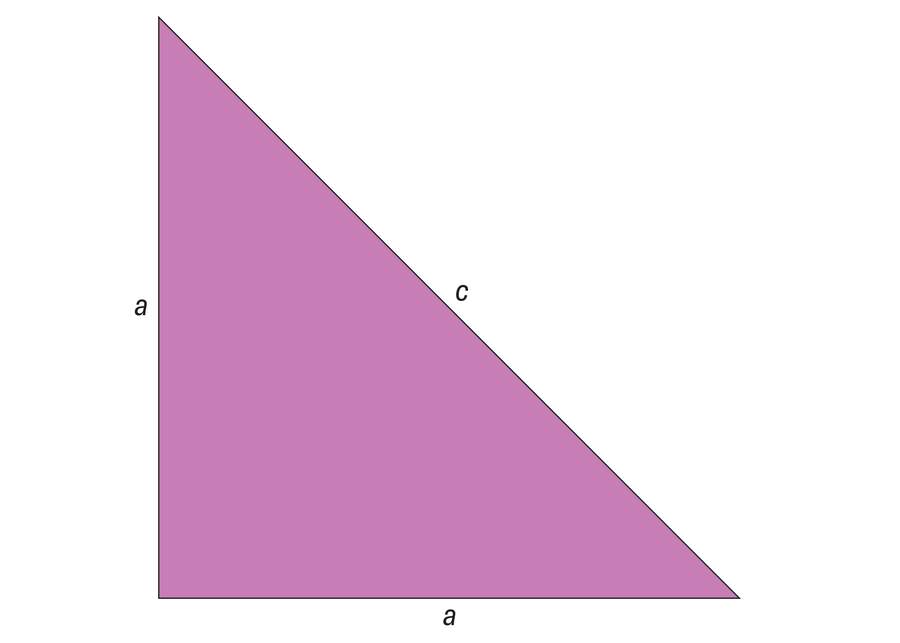
The existence of irrational numbers is greatest defined with an isosceles proper triangle—that’s, a triangle with two sides of an equal size that kind a proper angle.
Manon Bischoff/Spektrum der Wissenschaft
Such a triangle has a set side ratio a⁄c. If each a and c are rational numbers, the lengths of the edges of the triangle will be chosen in order that a and c every correspond to the smallest potential pure quantity (that’s, they don’t have any frequent divisor). For instance, if the side ratio had been 2/3 , you’ll select a = 2 and c = 3. Assuming that the lengths of the triangle correspond to rational numbers, a and c are integers and don’t have any frequent divisor—or so everybody thought.
Proof by Contradiction
Hippasus used this line of pondering to create a contradiction, which in flip proved that the unique assumption should be improper. First, he used the Pythagorean theorem (good outdated a2 + b2 = c2) to specific the size of the hypotenuse c as a perform of the 2 equal sides a. Or, to place that mathematically: 2a2 = c2. As a result of a and c are integers, it follows from the earlier equation that c2 should be an excellent quantity. Accordingly, c can also be divisible by 2: c = 2n, the place n is a pure quantity.
Substituting c = 2n into the unique equation provides: 2a2 = (2n)2 = 4n2. The two will be diminished on either side, giving the next end result: a2 = 2n2. As a result of a can also be an integer, it follows that a is squared and due to this fact is an excellent quantity. This conclusion contradicts the unique assumption, nonetheless, as a result of if a and c are each even, neither of them is usually a divisor.
This contradiction allowed Hippasus to conclude that the side ratio of an isosceles proper triangle a⁄c can’t correspond to a rational quantity. In different phrases, there are numbers that can’t be represented because the ratio of two integer values. For instance, if the correct angle forming sides a = 1, then the hypotenuse c = √2. And as we all know at present, √2 is an irrational quantity with decimal locations that proceed indefinitely with out ever repeating.
From our present perspective, the existence of irrational values doesn’t appear too stunning as a result of we’re confronted with this truth at a younger age. However we are able to solely think about what this realization might need prompted some 2,500 years in the past. It may have turned the mathematical worldview the wrong way up. So it’s no marvel that there are such a lot of myths and legends about its discovery.
This text initially appeared in Spektrum der Wissenschaft and was reproduced with permission.

